세그먼트 트리(Segment Tree)
트리 구조로 구간합을 구한다.
트리 구조로 구간 합을 구하기 때문에 시간 복잡도 O(logN)을 가진다.
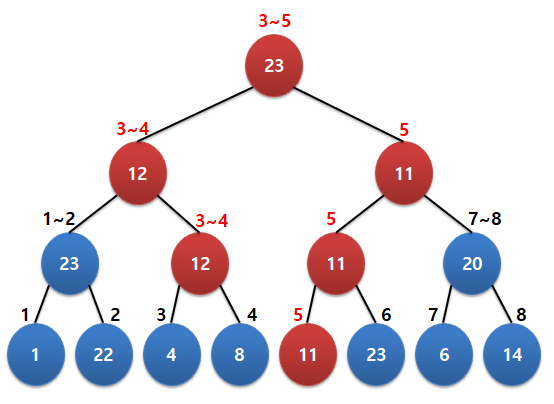
구간합 트리
완전 이진형태를 가지며 각 노드들은 특정 범위 인덱스의 구간합을 저장한다.
구간합
여러개의 데이터가 연속적으로 존재할 때, 특정한 범위의 데이터의 합을 구함
선형적으로 구간합을 구하면 O(N)의 시간 복잡도를 가짐
#include <stdio.h>
#include <stdlib.h>
#define NUMBER 7
int a[]={7, 1, 9, 5, 6, 4, 1};
int tree[4*NUMBER];
int init(int start, int end, int node){
if(start==end) return tree[node]=a[start];
int mid=(start+end)/2;
return tree[node]=init(start, mid, node*2)+init(mid+1, end, node*2+1);
}
int sum(int start, int end, int node, int left, int right){
if(left>end || right<start) return 0;
if(left<=start && end<=start)return tree[node];
int mid=(start+end)/2;
return sum(start, mid, node*2, left, right)+sum(mid+1, end, node*2+1, left, right);
}
void update(int start, int end, int node, int index, int dif){
if(index<start||index>end)return;
tree[node]+=dif;
if(start==end)return;
int mid=(start+end)/2;
update(start, mid, node*2, index, dif);
update(mid+1, end, node *2+1, index, dif);
}
int main(void){
init(0, NUMBER-1, 1);
printf("0부터 6까지의 구간 합: %d\n", sum(0, NUMBER-1, 1, 0, 6));
printf("인덱스 5의 원소를 +3만큼 수정\n");
update(0, NUMBER-1, 1, 5, 3);
printf("3부터 6까지의 구간 합: %d\n", sum(0, NUMBER-1, 1, 3, 6));
system("pause");
return 0;
}
세그먼트 트리에서의 구간 합 계산 및 원소 수정 과정은 O(logN)의 시간 복잡도를 가진다.